I’m starting to get back into writing up challenges and documenting my analysis. This was a simple 64-bit ELF binary with clear logic from crackmes.one. Here’s a breakdown of how I approached it.

Link: https://crackmes.one/crackme/6784563e4d850ac5f7dc5137
Binary: crackme (64-bit ELF)

Initial Observation

Running strings on the binary immediately reveals a few interesting strings:

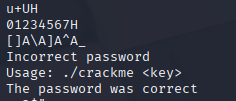
Checking the imports in Ghidra shows only a few basic functions:

Disassembly Notes

Disassembly of this binary in Ghidra was straightforward. No antidebugging or anti-reversing techniques were present.

After printing a usage string, the program checks if the user input is between 5 and 254 characters:

It then verifies that all input characters are digits using strspn:

After this validation, two key functions handle the logic behind validating the input, check_id_xor, and check_id_sum. Note that the binary copies the user’s input to &PASS:

check_id_xor

This function subtracts 48 from both the total input and the last digit, then XORs them:

check_id_sum

This function iterates through each character in the input, converts it to a number, and sums them. It expects this sum to equal the result of the XOR function:

First Attempt: Incorrect Assumptions

With the initial understanding, I wrote a brute-force script that performed the same operations as the binary and stopped once it found a match (xored == sum):

a = 0
while True:
    inp = str(a)

	# Ensure the length is at least 4
    while len(inp) < 5:
        inp = "0" + inp

	# Convert to integer and list of numbers
    inp_int = int(inp)
    inp_list = []
    for i in inp:
        inp_list.append(int(i))

	# XOR
    xored = (inp_int - 48) ^ (inp_list[-1] - 48)

	# SUM
    s = 0
    for i in range(len(inp_list)):
        x = 0
        if i == 0:
            x = -(inp_list[i] - 48)
        else:
            x = inp_list[i] - 48
        
        s += x

    print(xored, s)

    if xored == s:
        print("FOUND ", inp)
        break
    else:
        a += 1

This yielded 00213, but the binary rejected it:

Deeper Dive with IDA

Opening the binary in IDA made the real logic clearer.

Only the first and last digits are XORed (not the entire number!):

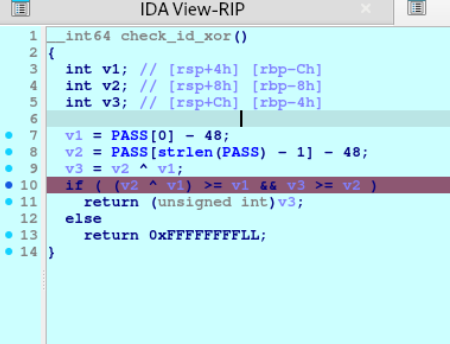
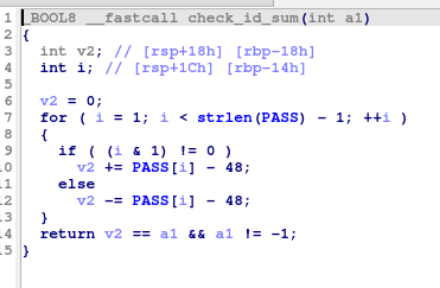
Sum logic is dependent on index parity:

• Subtract on even indices
• Add on odd indices

Finally, The -48 operation is just converting ASCII to integers ('0' = 48).

Fixed Cracker

With the correct understanding, I rewrote the script:

def check_id_xor(inp_list):
    a = inp_list[0]
    b = inp_list[-1]

    xored = b ^ a

    bad_num = True
    if (b ^ a) >= a and xored >= b:
        bad_num = False

    return xored, bad_num

def check_id_sum(inp_list):
    s = 0
    for i in range(len(inp_list)):
        if i & 1 == 0: # Even
            s -= inp_list[i]
        else:
            s += inp_list[i]
    return s

a = 0
while True:
    inp = str(a)
    while len(inp) < 5:
        inp = "0" + inp
    inp_int = int(inp)
    inp_list = []
    for i in inp:
        inp_list.append(int(i))

    xored, bad_num = check_id_xor(inp_list)
    if bad_num:
        a+=1
        continue

    s = check_id_sum(inp_list)

    print(xored, s)
    if xored == s:
        print("FOUND ", inp)
        break
    else:
        a += 1

Running this yields the correct solution: 00000

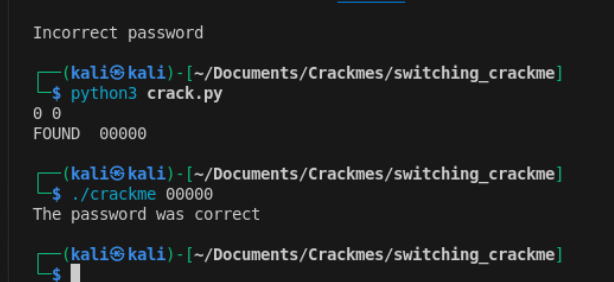
Conclusion

This was a fun, simple challenge with a straightforward key-gen solution. My initial mistakes came from assuming too much about how the XOR was calculated. A quick look in IDA helped clarify the logic and fix the brute-force script.

This serves as a great example of how taking time to reanalyze assumptions — and verifying details like which bytes are being operated on — can make or break your reverse engineering process.